In March, we released the zkVM 3.0, this post goes into more detail about its design intent and features.
The landscape of zero-knowledge virtual machines (zkVMs) is evolving quickly, driven by the demand for scalable, efficient, and reliable systems that can prove the correct execution of arbitrary programs regardless of computation size, programming language, or underlying architecture.
At Nexus, this vision led to the release of zkVM 3.0, a thoughtfully redesigned virtual machine that addresses long-standing limitations and introduces key innovations for the next generation of zero-knowledge virtual machines.
With zkVM 3.0, we introduced several architectural advancements, including a two-pass execution model, offline memory checking via logarithmic derivatives, and integration with the S-two prover.
These changes aim to improve proof efficiency, reduce memory overhead, and lay the groundwork for a modular and scalable system. Most importantly, zkVM 3.0 builds on the lessons of its predecessors and sets the stage for distributed and a la carte proving in future versions.
Foundations: zkVM 1.0 and 2.0
The initial versions of the Nexus zkVM laid important groundwork for scalable, verifiable computation.
zkVM 1.0 introduced a general-purpose recursive zero-knowledge virtual machine, leveraging folding-based proof systems such as Nova, SuperNova, and CycleFold.
These systems demonstrated the feasibility of incrementally verifiable computation (IVC), allowing for succinct proofs of arbitrarily long program executions. The architecture adopted the RISC-V RV32I instruction set, enabling compatibility with standard compiler toolchains, and showcased the power of recursion for large-scale computation.
Building on this foundation, zkVM 2.0 extended the architecture with support for HyperNova and integrated Jolt, a proving system driven by the Lasso lookup argument.
These enhancements improved frontend expressiveness and proof composition. The versions based on Nova and HyperNova also adopted a folding-based approach to recursion that was elegant and expressive, with support for complex programs and low memory overhead.
However, these designs also faced challenges. Memory checking of our folding-based recursive proof systems relied on Merkle tries, which, while secure and well-understood, introduced performance overhead and limited scalability.
Additionally, our folding-based proof systems were implementing a uniform IVC scheme that didn’t support cost modularity—meaning all instruction paths incurred similar proving costs regardless of usage. The reliance on the Grumpkin elliptic curve cycle, while enabling recursive composition, also brought additional complexity due to the need for non-native field arithmetic. Lastly, both versions depended on a trusted setup due to their use of the KZG polynomial commitment scheme by Kate, Zaverucha, and Goldberg.
Despite these trade-offs, zkVM 1.0 and 2.0 played a critical role in advancing the field of general-purpose zkVMs, and provided a robust base for the innovations introduced in zkVM 3.0.
zkVM 3.0: A refined architecture for scalable proofs
With zkVM 3.0, we build on the foundation of earlier versions and introduce a redesigned architecture that enhances efficiency and modularity of our proof system. This release allows us to address the key limitations of our prior implementations and offer a more scalable, developer-friendly platform for verifiable computation.
By shifting our focus toward scalability and flexibility, we introduced a set of key innovations that streamline performance and expand the system’s capabilities:
Offline memory checking with LogUps
We replaced Merkle-tree-based memory checking with a new technique based on logarithmic derivatives, known as LogUps. This approach allows us to track and verify memory access patterns without storing or managing the entire memory state during execution.
Instead, we maintain compact digests that summarize memory read/write operations efficiently. This significantly reduces proof complexity and enables us to validate memory in a stateless and scalable manner.
Two-pass execution model
zkVM 3.0 introduces a two-phase execution model to improve trace generation. In the first pass, the zkVM executes the program to gather memory usage and execution statistics, helping us establish a fixed memory layout.
In the second pass, the zkVM re-executes the program deterministically under this layout to produce a concise and optimized trace. This strategy helps us reduce unnecessary trace data and enables precise constraint encoding, improving both prover performance and verifier efficiency.
Integration of the S-two prover
To avoid the need for a trusted setup and improve proof performance, we integrated S-two, a transparent STARK prover developed by StarkWare. S-two uses a hash-based commitment scheme and supports Algebraic Intermediate Representations (AIR), which we use to encode zkVM constraints.
This choice enhances security, simplifies deployment, and additionally provides plausible post-quantum security.
Transition to small fields (M31)
We moved zkVM 3.0’s execution field to the Mersenne prime field (M31) used by S-two, which enables fast native arithmetic on 32-bit architectures.
This transition reduces commitment overheads and avoids the need for non-native arithmetic conversions, streamlining constraint generation and evaluation. It also ensures that both proving and verification steps benefit from hardware acceleration and more compact trace representations.
Support for RISC-V RV32I
Our zkVM’s instruction set is based on RISC-V RV32I, a widely adopted open ISA. This decision ensures that developers can leverage standard toolchains and familiar compiler infrastructure with minimal adjustment. It also facilitates future extensions and enhances portability for real-world applications.
Component-based architecture
We restructured the zkVM trace matrix to follow a component-based model. More specifically, the execution trace is now divided into logical units — CPU, register memory, program memory, data memory, and execution logic — each responsible for a distinct part of the trace.
This design enables modularity, simplifies future extensions (like distributed proving), and sets the stage for a la carte cost profiles where developers only pay for the features their programs actually use.
zkVM 3.0 components
We structure execution trace of zkVM 3.0 as a unified matrix, where each row corresponds to a single instruction cycle, and each column tracks the state of a specific variable or subcomponent. This trace captures the full state evolution of the virtual machine and forms the foundation of the proof that the zkVM outputs.
To support modularity and clear semantics, the trace is conceptually divided into the following components:
CPU
The CPU component is responsible for fetching, decoding, and preparing instructions for execution. It includes trace columns such as:
The current program counter (PC)
The decoded opcode
Control flags for instruction classification and branching behavior
This component ensures that the program advances correctly through its instruction stream and enforces rules around jump targets and halting.
Register memory
This component models the virtual machine’s general-purpose register file, used for storing intermediate and long-lived values. It includes:
Values of all registers at each cycle
Flags for read/write operations
Constraints to ensure data consistency between reads, writes, and executions
Register memory enforces correct register usage across arithmetic, logical, and memory instructions.
Program memory
Program memory is read-only and stores the byte-addressable instruction stream. Columns here are used to:
Represent byte-level contents of the program
Support instruction fetching logic (via memory read constraints)
Enforce a Harvard architecture separation from data memory
This allows the verifier to confirm that each instruction was fetched from the committed program region.
Data memory
Data memory handles read-write access to memory during program execution. It is used for stack operations, heap allocation, and memory-based computations.
Its trace columns track:
Memory addresses and values read/written per cycle
Access patterns used in offline memory checking
LogUp-based constraints to verify digest correctness
Unlike program memory, data memory is dynamic and its access patterns are determined by values computed during execution.
Instruction execution
This component governs instruction-specific semantics. It includes:
Input/output operands for each instruction
Flags that define the instruction type (e.g., ALU, memory, control flow)
Enforcement of arithmetic and logical constraints
Each row activates constraints corresponding to a specific instruction opcode, ensuring that it performs the correct computation with valid inputs.
These components are not physically separated in the trace matrix but are logically delineated for clarity. Internally, zkVM 3.0 represents them using shared and specialized columns, enabling efficient constraint composition while maintaining modular semantics. This organization also provides a clear path toward per-component proving in future versions.
Arithmetization example overview
To illustrate how zkVM 3.0 constructs a verifiable proof of execution, consider a simple RISC-V program running within the virtual machine. The arithmetization process translates this program’s behavior into a structured execution trace, which can then be verified using algebraic constraints.
Execution trace as a matrix
zkVM 3.0 represents the execution of a program as a large matrix, where:
Each row corresponds to one cycle of instruction execution.
Each column represents a state variable or a control signal used by one of the zkVM components (CPU, memory, execution logic, etc.).
This trace captures:
The program counter and the instruction being executed
The register values before and after execution
The memory addresses and data values read from or written to
Intermediate signals for decoding, branching, and arithmetic
The matrix evolves row by row as the program runs, producing a complete record of computation.
See the diagram below for a visual layout of this matrix and its logical organization.
Constraint systems via AIR
The correctness of this trace is enforced using an Algebraic Intermediate Representation (AIR). This system defines algebraic transition constraints (relating state at time t to t+1) and boundary constraints (e.g., input/output conditions).
For example:
A transition constraint for ALU instructions such as ADD ensures that the program counter (PC) increments by 4 between rows. That is, if row i corresponds to an ADD, then PC[i+1] = PC[i] + 4. This matches RISC-V semantics, where most instructions occupy 4 bytes.
A boundary constraint ensures that the PC starts at the correct entry point (usually 0) and satisfies a halting condition at the end of execution.
Each of these constraints is expressed as a low-degree polynomial over a finite field (M31 in zkVM 3.0), allowing them to be enforced efficiently within a S-two proof.
Subsets of columns and constraints
Not every column is active on every row:
Some columns are only relevant for instruction fetch, memory read/write, or arithmetic operations.
zkVM organizes these columns into logical components, allowing specific constraints to activate only when needed.
This structure minimizes constraint overhead while maintaining full expressiveness.
Refer to the diagram below to see how different components could map to subsets of columns within the unified trace.
Digest-based memory constraints
To avoid expensive Merkle proofs, zkVM 3.0 uses offline memory checking via LogUps. Rather than representing memory as a full state vector, zkVM builds polynomial constraints that validate memory access digests:
The trace includes the memory addresses and access types.
A separate digest row is maintained and updated using algebraic rules.
Constraints ensure that this digest behaves correctly across time steps.
This lets zkVM validate memory usage algebraically without holding memory in full.
This arithmetization strategy ensures that zkVM 3.0 can convert real-world computation into a compact, verifiable proof without compromising on generality or performance. It also sets the foundation for future modular and distributed proving architectures.
Current zkVM 3.0 limitations
Despite the substantial architectural upgrades in zkVM 3.0, certain core limitations remain. These trade-offs reflect the challenges of a fast - evolving system and inform our ongoing roadmap. As we continue to develop the zkVM, our focus is on modularity, scalability, and adaptability — ensuring that the system can flex to meet the needs of increasingly complex and distributed applications.
The following design choices in zkVM 3.0 highlight both the gains made and the opportunities ahead:
Monolithic trace
All components share a single trace matrix, leading to larger proofs due to unused columns, tight global coupling, and limited flexibility for component-level customization.
No modular proofs
zkVM currently produces one unified proof, restricting parallel or distributed proving, subcomponent reuse, and composability across modular program stages.
Uniform instruction cost
Each instruction imposes a similar overhead on the trace, which prevents usage-based optimization and poses challenges in resource-sensitive deployments.
Constraint complexity
Although AIR-based constraints offer expressive power, they can produce high-degree polynomials and increase inter-component dependencies.
Our priority with the next iteration of the zkVM is to introduce modular proofs, customizable cost profiles, and distributed proof generation — giving developers more control, efficiency, and scalability across varied environments.
Our vision for future zkVMs: Modular and distributed proving
As we look ahead to the next iteration of zkVM, our goal is to move beyond the monolithic architecture of zkVM 3.0 and embrace a more modular, scalable design.
We plan to decompose the single trace matrix into per-component traces, where each trace captures the behavior of an isolated subsystem — such as the CPU, memory, or arithmetic logic unit. Each of these traces will come with its own set of constraints and its own proof. To maintain global consistency, we’ll link shared variables across components using LogUp-based digest constraints**.
Modular component traces
By separating components, we enable:
Parallelized proof generation, where each subsystem can be proven independently and concurrently.
A la carte costing, allowing developers to pay only for the components their program actually uses.
Targeted optimization, as we can fine-tune constraint systems for each component based on its specific semantics and frequency of use.
Instruction-level decomposition
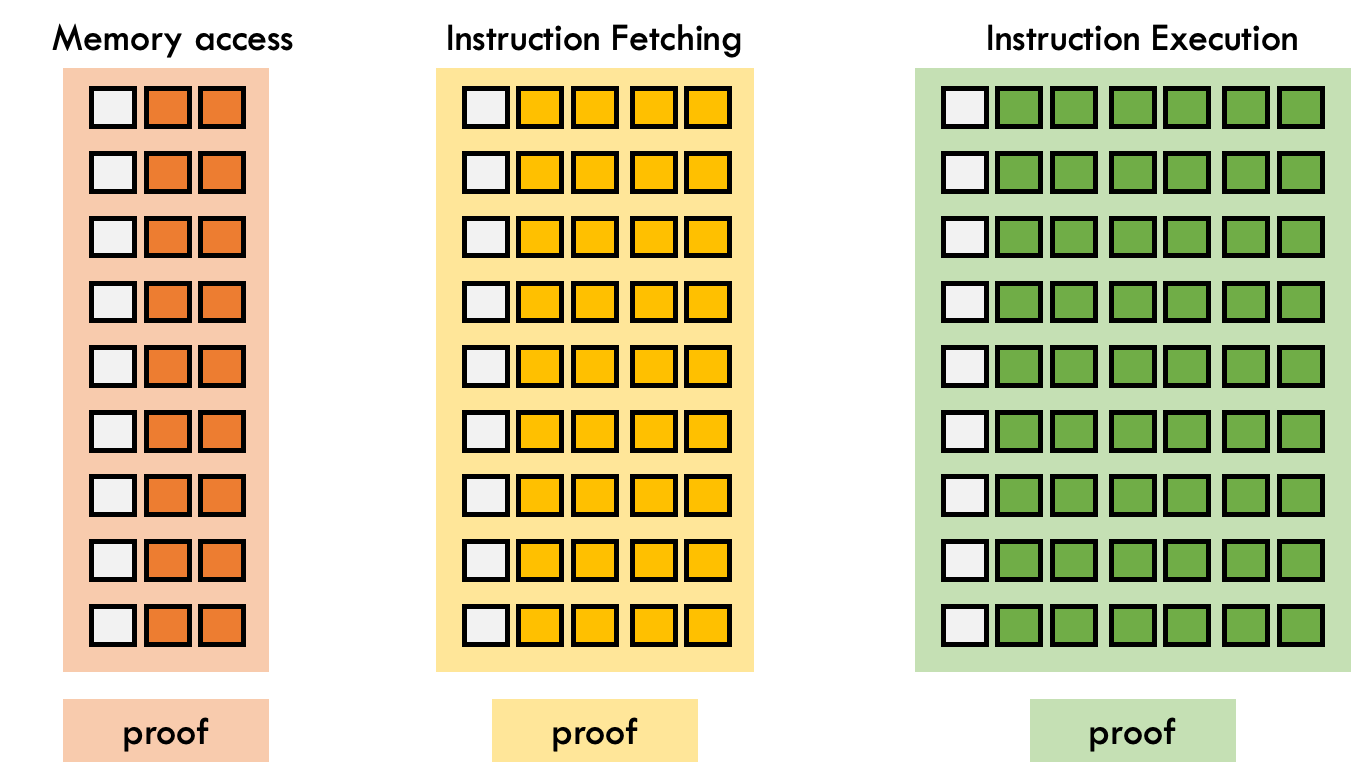
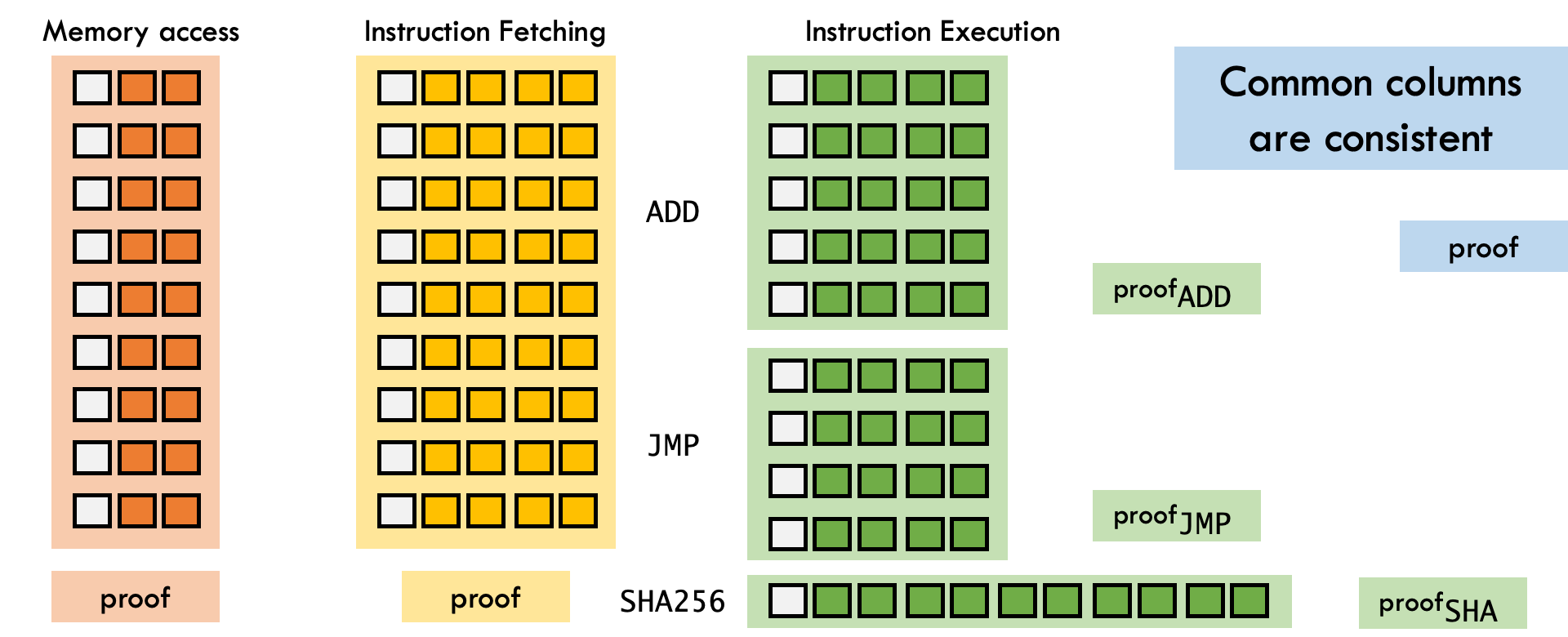
In addition to separating major subsystems, we intend to isolate instruction-level execution logic into shallow, specialized trace segments. For example, instructions like ADD, JUMP, or SHA256 can be handled in lightweight subcomponents that are only activated when relevant. This will allow us to:
Minimize trace size for common programs.
Lower polynomial degrees and number of constraints.
Support instruction set extensibility with minimal impact on the overall system.
Through this evolution, we aim to make future iterations of our zkVM more scalable, customizable, and developer-friendly, while preserving the generality and security guarantees that define the current version of our zkVM.
Expected outcomes
Full modularity with optional components
Support for precompiles and new instruction sets
Efficient reuse across circuits
Parallel proving and trace compression
Transparent, hash-based security
Conclusion
With zkVM 3.0, we’ve taken a meaningful step toward building a fast and modular zero-knowledge virtual machine. By integrating small-field arithmetic, offline memory checking, and the S-two prover, we’ve designed a system that balances performance with general-purpose flexibility.
At the same time, we recognize the architectural constraints that remain—from monolithic trace composition to fixed-cost instruction encoding. These lessons directly inform our roadmap for future iterations of our zkVM, where we plan to introduce modular proving, component isolation, and distributed proof generation.
We’re committed to building a zkVM that developers can scale with, adapt to their needs, and use confidently in high-integrity environments. zkVM 3.0 is the foundation—we’re excited to keep building from here.
