We're thrilled to announce the Nexus and Polyhedra Network partnership to build a hyper-parallel and ultra-performant zkVM powered by the GKR protocol.

Polyhedra consistently pushes cutting-edge ZK products to market. Emerging from the foundational zkBridge paper [1] developed in collaboration with Dawn Song at Berkeley and Dan Boneh at Stanford, Polyhedra has now added the Expander GKR prover which is already showing its incredible performance on critical ZK workloads like keccak-f permutations.

We've known their incredible team, led by Tiancheng Xie and Zhenfei Zhang, for years and couldn’t be more excited to work with them on pushing the frontiers of verifiable computation.

“We are thrilled that the Nexus team has partnered with us to bring Expander’s record-breaking zero-knowledge proof generation performance to the Nexus zkVM. Building a new, verifiable Internet is an audacious goal and one we are excited to contribute to. We look forward to continued collaboration with the Nexus team, pushing the boundaries of what is possible with zero-knowledge technology and the GKR protocol.” - Tiancheng Xie, Co-founder, CTO Polyhedra Network

The GKR Protocol

The GKR prover is known for its speed proving large computations, all while being well-suited for large-scale parallel computing. Invented by the legendary Shafi Goldwasser in collaboration with Kalai and Rothblum [2], and later improved by Thaler, Xie, Zhang and others, the Nexus and Polyhedra partnership will bring decades of research and engineering to life.

The SumCheck Protocol

The main primitive used within the GKR protocol is the sumcheck protocol, introduced by Lund, Fortnow, Karloff and Nisan [3] and based on the sumcalc protocol by Beaver and Feigenbaum [4].

The sumcheck protocol, discussed in depth in the Nexus 1.0 Whitepaper, allows a prover $\mathcal{P}$, to convince a verifier $\mathcal{V}$, that the sum of evaluations of a polynomial $g$ over an $\ell$-dimensional Boolean hypercube is correct.

$$T = \sum_{x_1 \in \{0, 1\}} \sum_{x_2 \in \{0, 1\}} \dots \sum_{x_\ell \in \{0, 1\}} g(x_1, x_2, \dots, x_\ell),$$

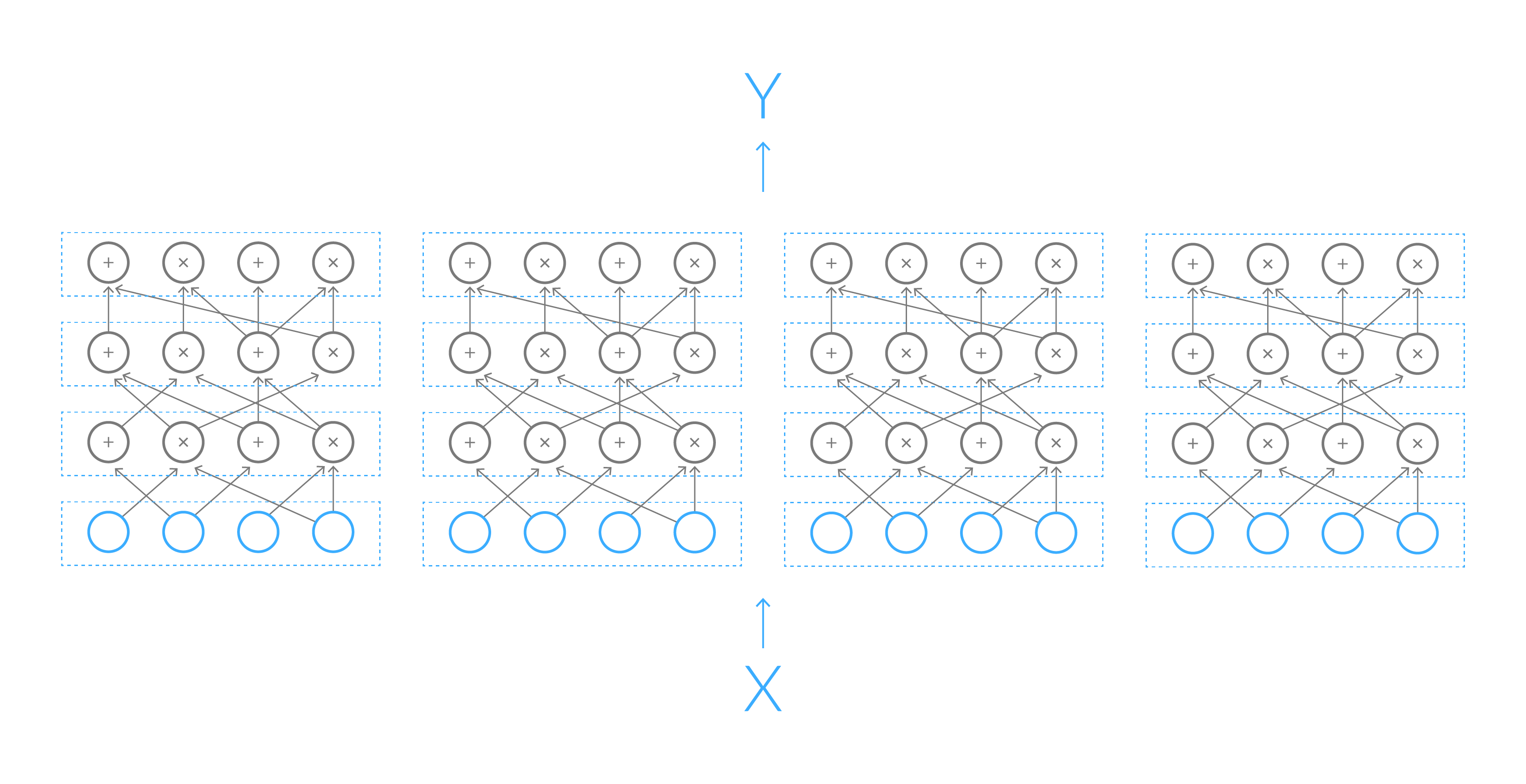
At a high level, the GKR protocol begins with encoding a general computation as an arithmetic circuit (see Figure 1 above). It then interprets the arithmetic circuit as a polynomial over a multidimensional domain. Finally, it applies the sumcheck protocol to prove that polynomial's evaluation. See Figure 2 and the Libra paper [5] for an in-depth presentation of the math behind GKR.

The Expander Prover and the Nexus zkVM

Nexus is partnering with Polyhedra to integrate the Expander prover as a GKR prover module in the Nexus zkVM stack, coupling directly behind the arithmetization system. This integration will work smoothly in conjunction with other Nexus modules, such as precompiles and proof compression.

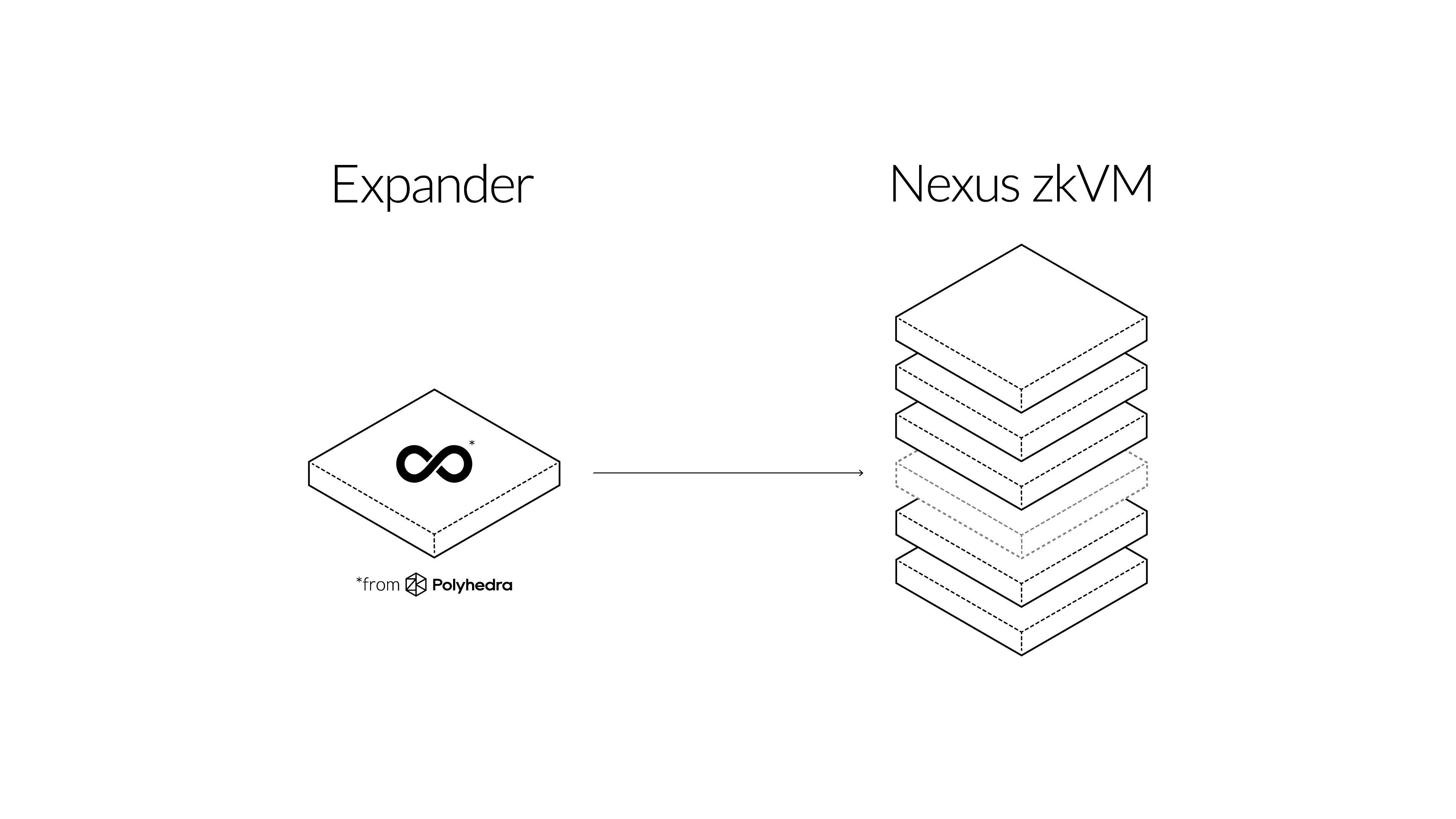
We are ecstatic about this partnership and happy to welcome Polyhedra to the Nexus ecosystem.

References

• [1] Tiacheng Xie, Jiaheng Zhang, Zerui Cheng, Fan Zhang, Yupeng Zhang, Yongzheng Jia, Dan Boneh, Dawn Song. 2022. ZkBridge: Trustless Cross-chain Bridges Made Practical. In Proceedings of the 2022 ACM SIGSAC Conference on Computer and Communications Security (CCS '22). Association for Computing Machinery, New York, NY, USA, 3003–3017.
• [2] Shafi Goldwasser, Yael Tauman Kalai, Guy N. Rothblum. 2015. Delegating Computation: Interactive Proofs for Muggles. J. ACM 62, 4, Article 27 (August 2015), 64 pages.
• [3] Carsten Lund, Lance Fortnow, Howard Karloff, Noam Nisan. 1992. Algebraic methods for interactive proof systems. J. ACM 39, 4 (Oct. 1992), 859–868.
• [4] Donald Beaver, Joan Feigenbaum. 1990. Hiding Instances in Multioracle Queries. In Proceedings of the 7th Annual Symposium on Theoretical Aspects of Computer Science (STACS '90). Springer-Verlag, Berlin, Heidelberg, 37–48.
• [5] Tiacheng Xie, Jiaheng Zhang, Yupeng Zhang, Charalampos Papamanthou, Dawn Song. 2019. Libra: Succinct Zero-Knowledge Proofs with Optimal Prover Computation. In Advances in Cryptology – CRYPTO 2019: 39th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 18–22, 2019, Proceedings, Part III. Springer-Verlag, Berlin, Heidelberg, 733–764.